Preliminaries
Boosting
The committee has an equal weight for every prediction from all models, and it gives little improvement than a single model. Then boosting was built for this problem. Boosting is a technique of combining multiple ‘base’ classifiers to produce a form of the committee that:
- performances better than any of the base classifiers and
- each base classifier has a different weight factor
Adaboost
Adaboost is short for adaptive boosting. It is a method combining several weak classifiers which are just better than random guesses and it gives a better performance than the committee. The base classifiers in AdaBoost are trained sequentially, and their training set is the same but with different weights for each sample. So when we consider the distribution of training data, every weak classifier was trained on different sample distribution. This might be an important reason for the improvement of AdaBoost from the committee. And the weights for weak classifiers are generated depending on the performance of the previous classifier.
During the prediction process, the input data flows from classifier to classifier and the final result is some kind of combination of all output of weak classifiers.
Important ideas in the AdaBoost algorithm are:
- the data points are predicted incorrectly in the current classifier giving a greater weight
- once the algorithm was trained, the prediction of each classifier is combined through a weighted majority voting scheme as:

where \(w_n^{(1)}\) is the initial weights of input data of the \(1\) st weak classifier, \(y_1(x)\) is the prediction of the \(1\) st weak classifier, \(\alpha_m\) is the weight of each prediction(notably this weight works to \(y_m(x)\) and \(w_n^{(1)}\) is the weight of input data of the first classifier.). And the final output is the sign function of the weighted sum of all predictions.
The procedure of the algorithm is:
- Initial data weighting coefficients \(\{\boldsymbol{w}_n\}\) by \(w_n^{(1)}=\frac{1}{N}\) for \(n=1,2,\cdots,N\)
- For \(m=1,\dots,M\):
- Fit a classifier \(y_m(\boldsymbol{x})\) to training set by minimizing the weighted error function: \[J_m=\sum_{}^{}w_n^{(m)}I(y_m(\boldsymbol{x}_n)\neq t_n)\] where \(I(y_m(\boldsymbol{x})\neq t_n)\) is the indicator function and equals 1 when \(y_m(\boldsymbol{x})\neq t_n\) and 0 otherwise
- Evaluate the quatities: \[\epsilon_m=\frac{\sum_{n=1}^Nw_n^{(m)}I(y_m(\boldsymbol{x})\neq t_n)}{\sum_{n=1}^{N}w_n^{(m)}}\] and then use this to evaluate \(\alpha_m=\ln \{\frac{1-\epsilon_m}{\epsilon_m}\}\)
- Updata the data weighting coefficients: \[w_n^{(m+1)}=w_n^{(m)}\exp\{\alpha_mI(y_m(\boldsymbol{x})\neq t_n)\}\]
- Make predictions using the final model, which is given by: \[Y_M = \mathrm{sign} (\sum_{m=1}^{M}\alpha_my_m(x))\]
This procedure comes from ‘Pattern recognition and machine learning’1
Python Code of Adaboost
# weak classifier
# test each dimension and each value and each direction to find a
# best threshold and direction('<' or '>')
class Stump():
def __init__(self):
self.feature = 0
self.threshold = 0
self.direction = '<'
def loss(self,y_hat, y, weights):
"""
:param y_hat: prediction
:param y: target
:param weights: weight of each data
:return: loss
"""
sum = 0
example_size = y.shape[0]
for i in range(example_size):
if y_hat[i] != y[i]:
sum += weights[i]
return sum
def test_in_traing(self, x, feature, threshold, direction='<'):
"""
test during training
:param x: input data
:param feature: classification on which dimension
:param threshold: threshold
:param direction: '<' or '>' to threshold
:return: classification result
"""
example_size = x.shape[0]
classification_result = -np.ones(example_size)
for i in range(example_size):
if direction == '<':
if x[i][feature] < threshold:
classification_result[i] = 1
else:
if x[i][feature] > threshold:
classification_result[i] = 1
return classification_result
def test(self,x):
"""
test during prediction
:param x: input
:return: classification result
"""
return self.test_in_traing(x, self.feature, self.threshold, self.direction)
def training(self, x, y, weights):
"""
main training process
:param x: input
:param y: target
:param weights: weights
:return: none
"""
example_size = x.shape[0]
example_dimension = x.shape[1]
loss_matrix_less = np.zeros(np.shape(x))
loss_matrix_more = np.zeros(np.shape(x))
for i in range(example_dimension):
for j in range(example_size):
results_ji_less = self.test_in_traing(x, i, x[j][i], '<')
results_ji_more = self.test_in_traing(x, i, x[j][i], '>')
loss_matrix_less[j][i] = self.loss(results_ji_less, y, weights)
loss_matrix_more[j][i] = self.loss(results_ji_more, y, weights)
loss_matrix_less_min = np.min(loss_matrix_less)
loss_matrix_more_min = np.min(loss_matrix_more)
if loss_matrix_less_min > loss_matrix_more_min:
minimum_position = np.where(loss_matrix_more == loss_matrix_more_min)
self.threshold = x[minimum_position[0][0]][minimum_position[1][0]]
self.feature = minimum_position[1][0]
self.direction = '>'
else:
minimum_position = np.where(loss_matrix_less == loss_matrix_less_min)
self.threshold = x[minimum_position[0][0]][minimum_position[1][0]]
self.feature = minimum_position[1][0]
self.direction = '<'
class Adaboost():
def __init__(self, maximum_classifier_size):
self.max_classifier_size = maximum_classifier_size
self.classifiers = []
self.alpha = np.ones(self.max_classifier_size)
def training(self, x, y, classifier_class):
"""
training adaboost main steps
:param x: input
:param y: target
:param classifier_class: what can classifier would be used, here we use stump above
:return: none
"""
example_size = x.shape[0]
weights = np.ones(example_size)/example_size
for i in range(self.max_classifier_size):
classifier = classifier_class()
classifier.training(x, y, weights)
test_res = classifier.test(x)
indicator = np.zeros(len(weights))
for j in range(len(indicator)):
if test_res[j] != y[j]:
indicator[j] = 1
cost_function = np.sum(weights*indicator)
epsilon = cost_function/np.sum(weights)
self.alpha[i] = np.log((1-epsilon)/epsilon)
self.classifiers.append(classifier)
weights = weights * np.exp(self.alpha[i]*indicator)
def predictor(self, x):
"""
prediction
:param x: input data
:return: prediction result
"""
example_size = x.shape[0]
results = np.zeros(example_size)
for i in range(example_size):
y = np.zeros(self.max_classifier_size)
for j in range(self.max_classifier_size):
y[j] = self.classifiers[j].test(x[i].reshape(1,-1))
results[i] = np.sign(np.sum(self.alpha*y))
return resultsthe entire project can be found https://github.com/Tony-Tan/ML. And please star me! Thanks!
When we use different numbers of classifiers, the results of the algorithm are like this:
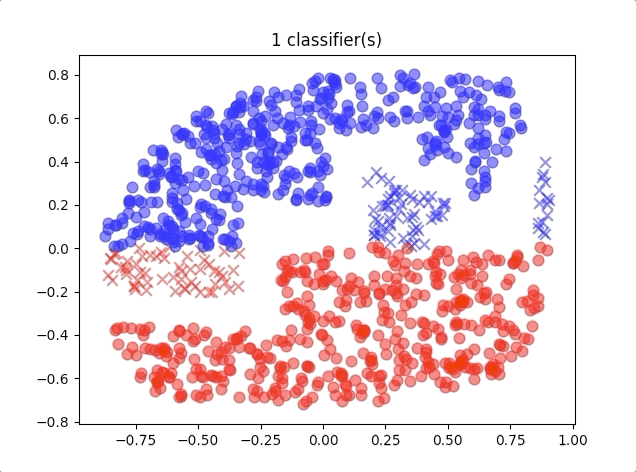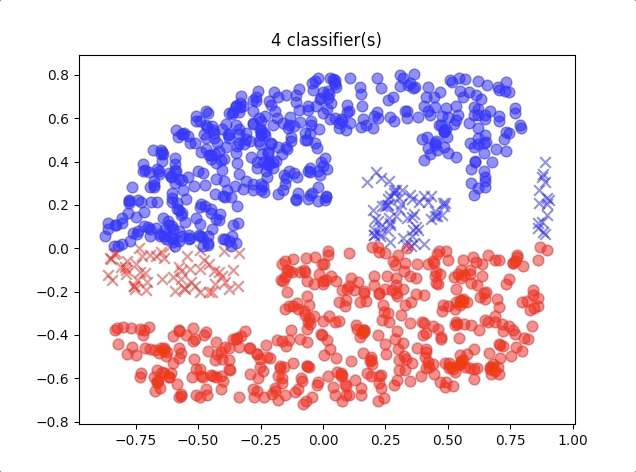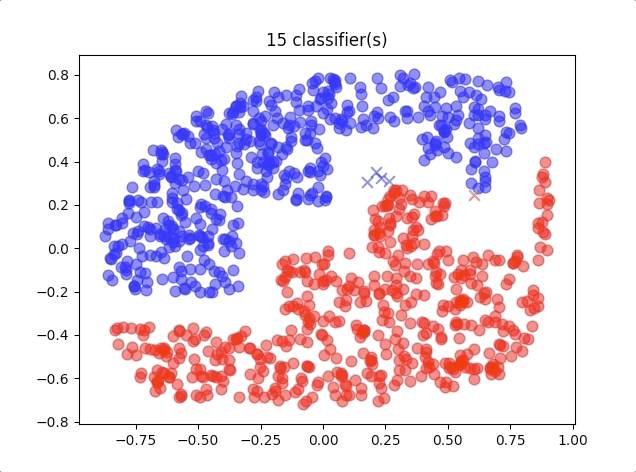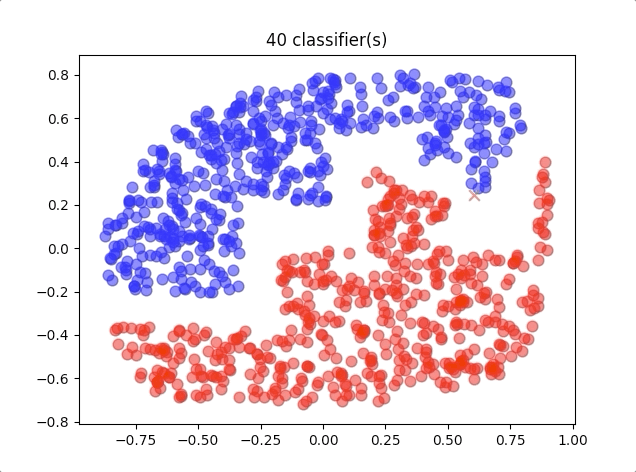
where the blue circles are the correct classification of class 1 and red circles are the correct classification of class 2. And the blue crosses belong to class 2 but were classified into class 1, and so do the red crosses.
A 40-classifiers AdaBoost gives a relatively good prediction:

where there is only one misclassified point.
References
Bishop, Christopher M. Pattern recognition and machine learning. springer, 2006.↩︎