Bayesian Model Averaging(BMA) and Combining Models

Preliminaries

1. Bayesian Theorem

Bayesian Model Averaging(BMA)¹

Bayesian model averaging(BMA) is another wildly used method that is very like a combining model. However, the difference between BMA and combining models is also significant.

A Bayesian model averaging is a Bayesian formula in which the random variable are models(hypothesizes) \(h=1,2,\cdots,H\) with prior probability \(\Pr(h)\), then the marginal distribution over data \(X\) is:

\[ \Pr(X)=\sum_{h=1}^{H}\Pr(X|h)\Pr(h) \]

And the MBA is used to select a model(hypothesis) that can model the data best through Bayesian theory. When we have a larger size of \(X\), the posterior probability

\[ \Pr(h|X)=\frac{\Pr(X|h)\Pr(h)}{\sum_{i=1}^{H}\Pr(X|i)\Pr(i)} \]

become sharper. Then we got a good hypothesis.

Mixture of Gaussian(Combining Models)

In post ‘Mixtures of Gaussians’, we have seen how a mixture of Gaussians works. Then the joint distribution of input data \(\mathbf{x}\) and latent variable \(\mathbf{z}\) is:

\[ \Pr(\mathbf{x},\mathbf{z}) \]

and the margin distribution of \(\mathbf{x}\) is

\[ \Pr(\mathbf{x})=\sum_{\mathbf{z}}\Pr(\mathbf{x},\mathbf{z}) \]

For the mixture of Gaussians: \[ \Pr(\mathbf{x})=\sum_{k=1}^{K}\pi_k\mathcal{N}(\mathbf{x}|\mathbf{\mu}_k,\Sigma_k) \] the latent variable \(\mathbf{z}\) is designed: \[ \Pr(z_k) = \pi_k \] for \(k=\{1,2,\cdots,K\}\). And \(z_k\in\{0,1\}\) is a \(1\)-of-\(K\) representation.

This mixture of Gaussians is a kind of combining models. Each time, only one \(k\) is selected(for \(\mathbf{z}\) is \(1\)-of-\(K\) representation). An example of a mixture of Gaussians, and its original curve is like:

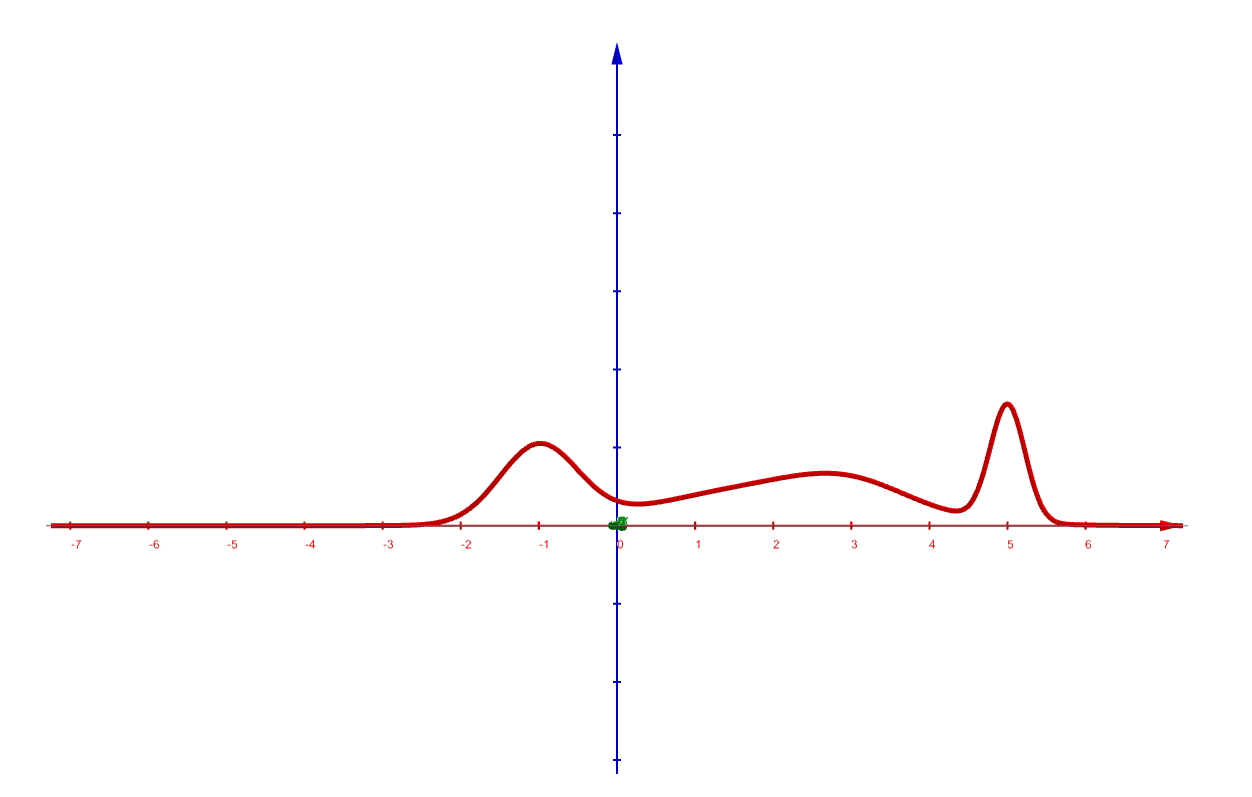
And the latent variables \(\mathbf{z}\) separate the whole distribution into several Gaussian distributions:

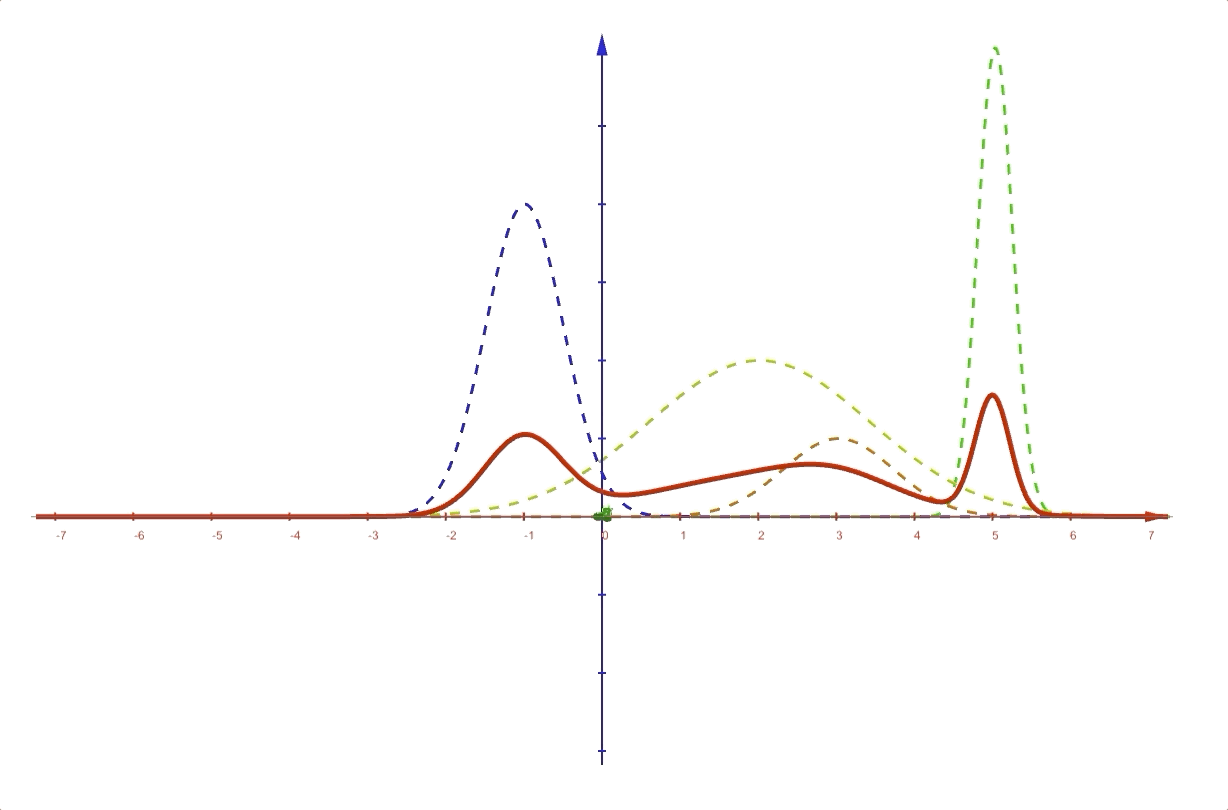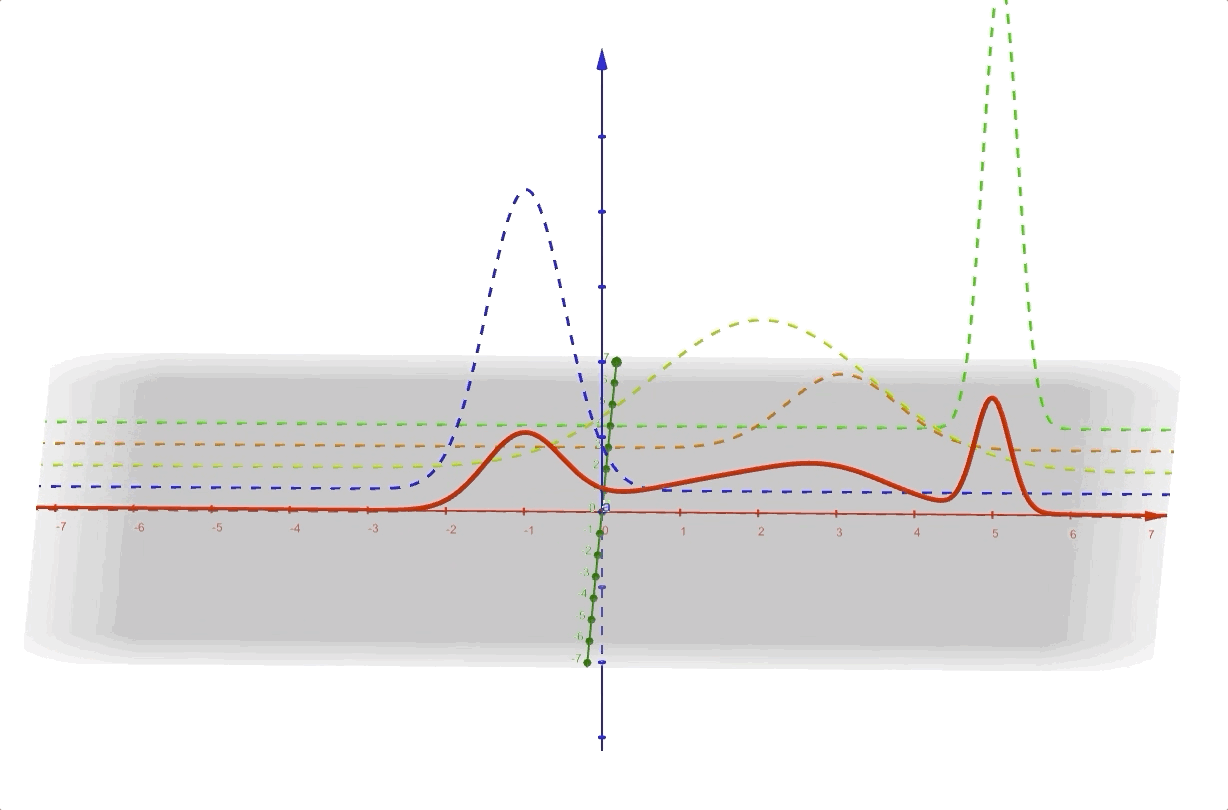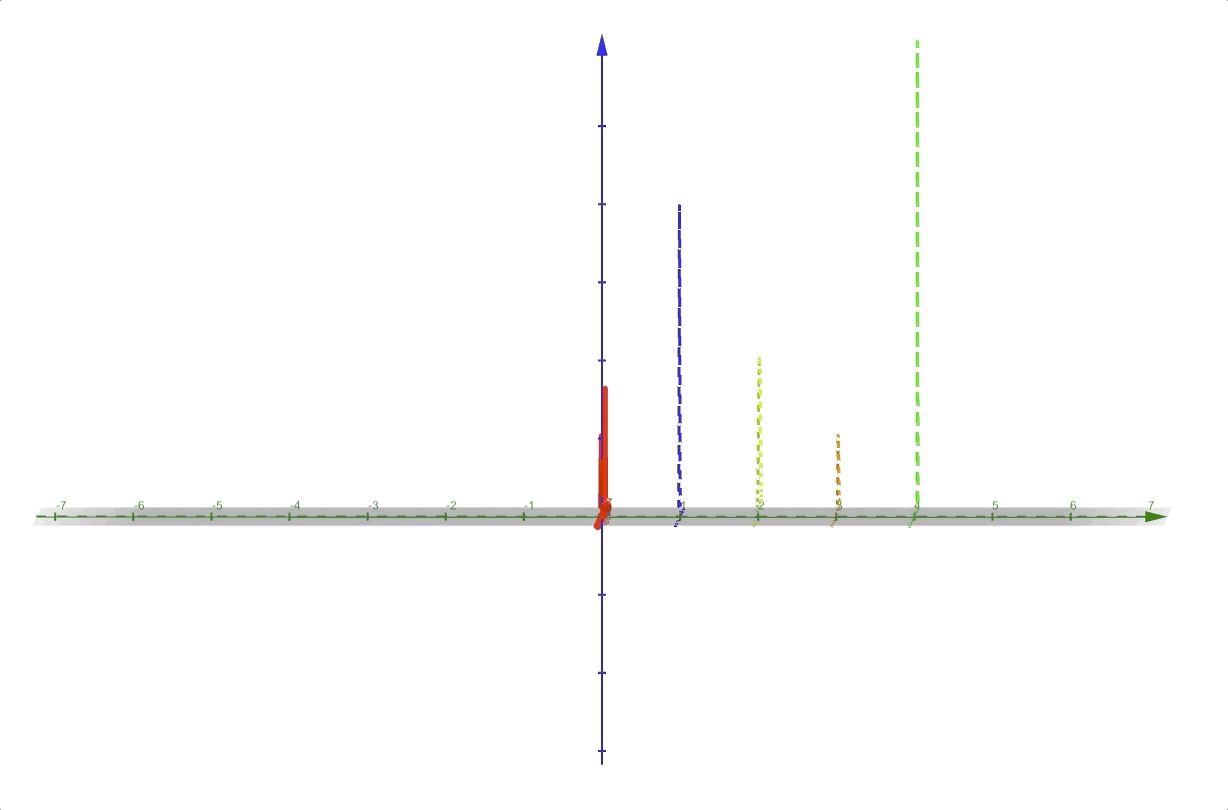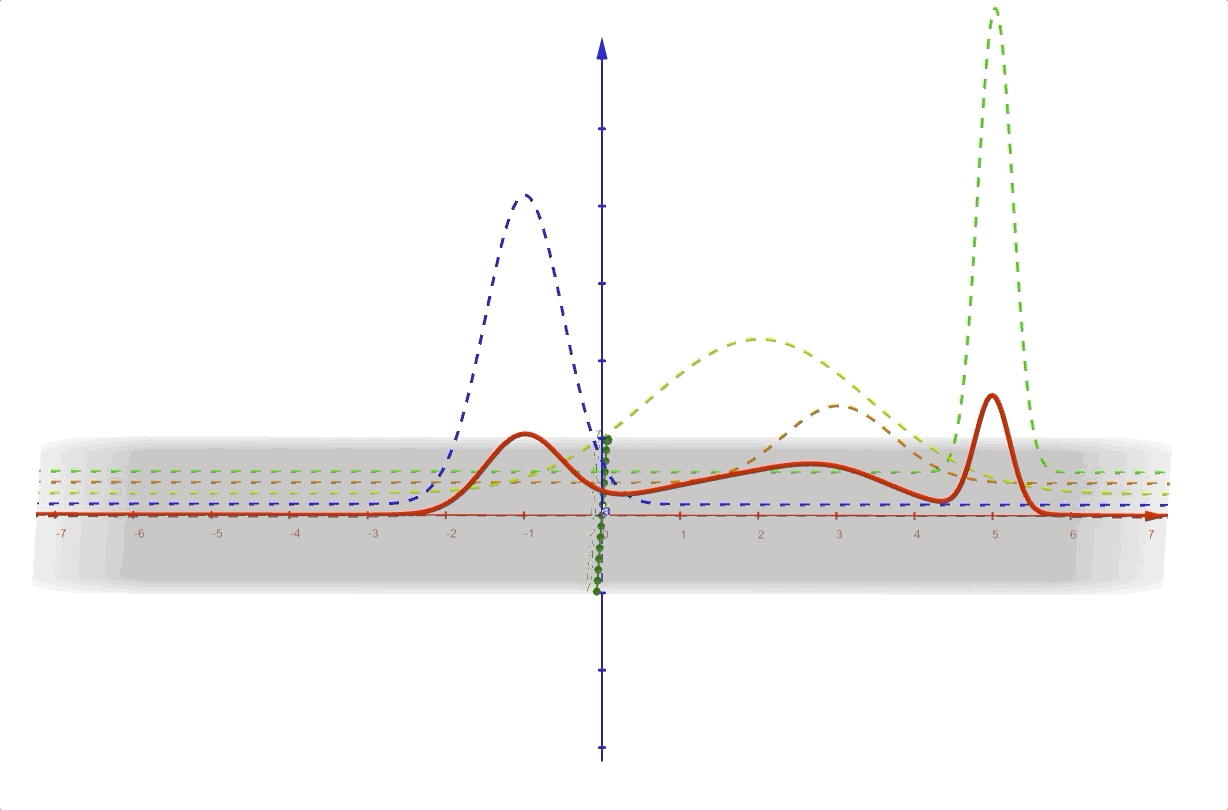
This is the simplest model of combining models where each expert is a Gaussian model. And during the voting, only one model was selected by \(\mathbf{z}\) to make the final decision.

Distinction between BMA and Combining Methods

A combining model method contains several models and predicts by voting or other rules. However, Bayesian model averaging can be used to generate a hypothesis from several candidates.

References